Finding Radius authentication password with a single Access-Request

This is a writeup about an uninted solution of a challenge based around the RADIUS protocol. We were provided with a pcap file of a Radius authentication trace and the goal was to find the used password.

The intended solution was actually to attempt a connexion against the radius server, crack the shared secret with a User-Password Attribute Based Shared Secret Attack and then recover the password. I managed to find the password without any interaction with the server, needing only the Access-Request packet given in the pcap trace.

Here is an exemple of the given trace:

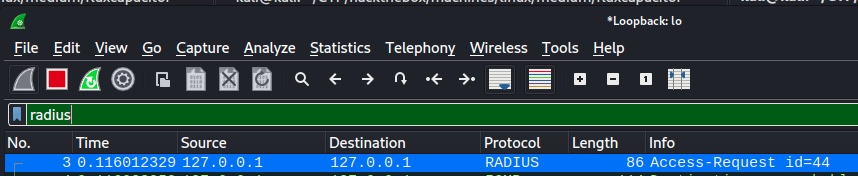
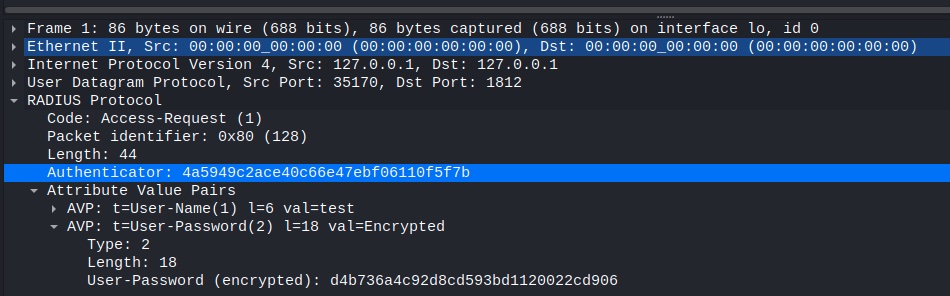
Radius protocol

The RADIUS (Remote Authentication Dial-In User Service) protocol is a networking protocol that provides centralized authentication, authorization, and accounting for users who connect and use a network service. It was developed by Livingston Enterprises, Inc., and is now maintained by the IETF (Internet Engineering Task Force) as a standard.

By looking at the RFC, we can see how the password-based authentication works:

The password is first padded at the end with nulls to a multiple of 16 octets.
A one-way MD5 hash is calculated over a stream of octets consisting of the shared secret followed by the Request Authenticator.
This value is XORed with the first 16 octet segment of the password and placed in the first 16 octets of the String field of the User-Password Attribute.

As for the pseudo-algorithm:

Call the shared secret S and the pseudo-random 128-bit Request Authenticator RA. Break the password into 16-octet chunks p1, p2, etc.
with the last one padded at the end with nulls to a 16-octet boundary.
Call the ciphertext blocks c(1), c(2), etc. We’ll need intermediate values b1, b2, etc.

     b1 = MD5(S + RA)       c(1) = p1 xor b1
     b2 = MD5(S + c(1))     c(2) = p2 xor b2
            .                       .
            .                       .
            .                       .
     bi = MD5(S + c(i-1))   c(i) = pi xor bi
     The String will contain c(1)+c(2)+…+c(i) where + denotes concatenation.

The strategy

Thanks to the RFC we can say that:

encrypted_password = plaintext_password ^ md5(shared_secret + authenticator)

So:

plaintext_password = encrypted_password ^ md5(shared_secret + authenticator)

Inputs:

encrypted_passowrd, authenticator are known.
We know that shared_secret is a small string (weak secret).
We know the password is no more than 16 characters long because of the length of the encrypted password (16 bytes) taken from the trace.

We will try to bruteforce the shared secret and generate all possible plain_text passwords by XORing the md5 hash with the encrypted password as shown above.

This is the key: we make the hypothesis that the plaintext password is an UTF8 String so trying to decode its byte stream shouldn’t fail. This operation enables us to filter a lot of possible plaintext password candidates.

To sum up :

We compute all the possible shared secret strings, and for each shared shecret:
- We concatenate the shared_secret with the authenticator, compute the md5 hash of the whole and then xor it againt the encrypted password
- We then try to decode the byte stream produced:
  - If it fails, then we move on to the next shared secret candidate
  - If it succeeds, then we may have found the plain text password.
    - To verify that we check that the utf8 decoded string is no more than 16 characters long and that it ends with padding. If it’s the case we print the possible password.
    - The worst case is that we find no padding, so we can’t know for sure whether it is the right password, so we print it anyway.

By doing so, we are able to find that different combination of plain text password and shared secrets can lead to the same authenticator string!

Here is the python script:

import sys
import hashlib
import string
import itertools

printable = [ord(i) for i in string.printable]
CHARSET = string.ascii_letters + string.digits

authenticator = bytes.fromhex("4a5949c2ace40c66e47ebf06110f5f7b")
pwd_encrypted = bytes.fromhex("d4b736a4c92d8cd593bd1120022cd906")

def xor_strings(str1, str2):
    return bytes.fromhex(hex(int(str1.hex(), 16) ^ int(str2.hex(), 16))[2:])


def check_word(word, shared):
    for i in range(15, -1, -1):
        pattern = b'\x00' * i
        if len(word) == 16 and word.endswith(pattern) and all(i in printable for i in word.replace(b'\x00', b'')):
            print(f"Word ending with {i} null bytes: {word},     shared_secret = {shared}")
            break


def find_possible_passwords(shared_secret_length):
    print(f"[*] Finding possible plain for shared secret of length : {shared_secret_length}")
    for combo in itertools.product(CHARSET, repeat=shared_secret_length):
        shared = ''.join(combo).encode()
        try:
            word = xor_strings(hashlib.md5(shared + authenticator).digest(), pwd_encrypted)
            word.decode()  
            check_word(word, shared)
        except Exception:
            continue


# Find possible plain passwords by bruteforcing shared secrets (increasing lentgh)
for i in range(1,5):  
    find_possible_passwords(i)

You can test it by capturing a Radius Access-Request and doing:

echo 'User-Name=test,User-Password=P@ssw0rds2042!' | radclient localhost:1812 auth 0fGd

python3 solve.py
[*] Finding possible plain for shared secret of length : 1
[*] Finding possible plain for shared secret of length : 2
[*] Finding possible plain for shared secret of length : 3
[*] Finding possible plain for shared secret of length : 4
Word ending with 0 null bytes: b'NHW|U<{D/`wgSnI\\',     shared_secret = b'ecpr'
Word ending with 0 null bytes: b'$v2\ndO_]dST9@`@R',     shared_secret = b'jpUp'
Word ending with 0 null bytes: b'_XX?~(I`$Lw]pxhs',     shared_secret = b'zqTv'
Word ending with 0 null bytes: b'iKZ\x00*-vFg6<CBm}z',     shared_secret = b'DnDi'
Word ending with 0 null bytes: b'naltj3\x005\x0b(_C\n[~l',     shared_secret = b'HiHS'
Word ending with 2 null bytes: b'P@ssw0rds2042!\x00\x00',     shared_secret = b'0fGd'

We recognize the password at the end with padding, and the shared secret!

Password more than 16 characters long

The previous case had a password with at most 16 characters. The next challenge was similar but with a password with more than 16 characters.

We actually used the same technique and because the password was more then 16 charaters long, it was easier to find!

Remember the Radius RFC pseudo algorighm for computing the encrypted password:

         b1 = MD5(S + RA)       c(1) = p1 xor b1
         b2 = MD5(S + c(1))     c(2) = p2 xor b2
                .                       .
                .                       .
                .                       .
         bi = MD5(S + c(i-1))   c(i) = pi xor bi

The String will contain c(1)+c(2)+...+c(i) where + denotes concatenation.
On receipt, the process is reversed to yield the original password.

The encrypted password hextstring is split in two :

pwd : pwd = pwd_1 + pwd_2

So we have

plain = p1 + p2
pwd2 = p2 ^ md5(shared + pwd1)             ==>   p2 = pwd2 ^ md5(shared + pwd1)
pwd1 = p1 ^ md5(shared + request_authent)  ==>   p1 = pwd1 ^ md5(shared + request_authent)

Here is the script:

import hashlib
import sys
import string
import itertools


CHARSET = string.ascii_letters + string.digits
printable = [ord(i) for i in string.printable]


authenticator_access_request_1  = bytes.fromhex("2387de87e7816cf298c77e818031a879" )
pwd_1                           = bytes.fromhex("4ed97da65122dc872ea89538e287a04e")
pwd_2                           = bytes.fromhex("3b4abe9227f4d43918b369c9449a107b")

def xor_strings(str1, str2):
    return bytes.fromhex(hex(int(str1.hex(), 16) ^ int(str2.hex(), 16))[2:])

def check_word(word, shared):
    for i in range(15, -1, -1):
        pattern = b'\x00' * i
        if len(word) == 16 and word.endswith(pattern) and all(i in printable for i in word.replace(b'\x00', b'')):
            print(f"Word ending with {i} null bytes: {word},     shared_secret = {shared}")
            break

def find_possible_passwords(shared_secret_length, authenticator, pwd_encrypted):
    for combo in itertools.product(CHARSET, repeat=shared_secret_length):
        shared = ''.join(combo).encode()
        try:
            word = xor_strings(hashlib.md5(shared + authenticator).digest(), pwd_encrypted)
            word.decode()   
            check_word(word, shared)
        except Exception:
            continue

# Find possible plain passwords by bruteforcing shared secrets (increasing lentgh)
for i in range(1,5):
    print(f"[*] Finding possible passwords for shared secret length of {i}")
    print(f"Computing second half of password")
    find_possible_passwords(i, pwd_1, pwd_2)

    print(f"computing first half of password")
    find_possible_passwords(i, authenticator_access_request_1, pwd_1)

Here is the output:

python3 solve2.py 
[*] Finding possible passwords for shared secret length of 1
Computing plain2
computing plain1
[*] Finding possible passwords for shared secret length of 2
Computing plain2
computing plain1
[*] Finding possible passwords for shared secret length of 3
Computing plain2
computing plain1
[*] Finding possible passwords for shared secret length of 4
Computing plain2
Word ending with 0 null bytes: b'I\x0cN0uKtv7mcgZAI`',     shared_secret = b'aAI4'
Word ending with 0 null bytes: b'|1i0Dq>b7,lC W(f',     shared_secret = b'oSxu'
Word ending with 0 null bytes: b'B8o$Q&iehAt\n@acl',     shared_secret = b't0Fq'
Word ending with 0 null bytes: b'Id $1N%jnIw"eX1H',     shared_secret = b'zXXu'
Word ending with 0 null bytes: b'2=q\nC<-OJ-t,jF6C',     shared_secret = b'KfvD'
Word ending with 0 null bytes: b'F\rccdu,w7:~6+n~&',     shared_secret = b'0iSJ'
Word ending with 7 null bytes: b'oeifklzmq\x00\x00\x00\x00\x00\x00\x00',     shared_secret = b'1fGd'
computing plain1
Word ending with 0 null bytes: b'JbUUkT6ih_<[G\t/G',     shared_secret = b'ekrc'
Word ending with 0 null bytes: b'}H^C)qJlG\rqx=|W]',     shared_secret = b'gCoP'
Word ending with 0 null bytes: b'^y@bIZaI]Z4AZ8N.',     shared_secret = b'kEGe'
Word ending with 0 null bytes: b"gS^x>\x0c'7>HX7[43J",     shared_secret = b'sTCK'
Word ending with 0 null bytes: b'klozf12jloiejflz',     shared_secret = b'1fGd'
Word ending with 0 null bytes: b'=Z=8B7=>0^"[e}<y',     shared_secret = b'1WZ2'

We see the second half of password with padding, and then the first half of the password with the same shared secret of course. I actually could improve the computing part of the password’s first half by only keeping candidates that have the same shared secrets than the second half. When I ran it the first time I immediately saw the padding and new it was the right password’s half and the right shared secret.

Conclusion

I had fun doing this challenge and only found at the end that the intended solution was actually to bruteforce the shared secret. With the presented technique I could recover the password and the shared secret at the same time. Remember:

Have strong password: this attack wouldn’t have been reasonably possible without a weak shared secret.
Don’t reuse secrets in order to limit the impact of credential leak.

Radius protocol#

The strategy#

Password more than 16 characters long#

Conclusion#

Radius protocol

The strategy

Password more than 16 characters long

Conclusion